Lineer regresyon, makine öğrenmesinin en eski yöntemlerinden olup, bir bağımlı değişken ile bir veya birden çok bağımsız değişken arasında ki ilişkiyi formülize etmek için kullanılan bir yöntemdir. Burada ki amacımız, minimum hataya sahip, bağımsız değişkenlerin bağımlı değişkenler üzerinde ki etkisini bulmaktır. Gerçek verilerden oluşan eğitim verisi kullanılarak, her bir değişkenin sonuç üzerindeki ağırlığı belirlenir ve daha sonra yeni gelen verilerle bir sonraki durum tahmin edilebilir. Örneğin, marketler zincirinizin olduğunu ve birçok şehirde şubelerinizin olduğunu düşünün. Yeni bir şube açacaksınız ama hangi şehirde? Karınızın o şehrin nüfusu ile bağlantılı olduğunu varsayarsak, elinizdeki eğitim verisini (şubelerinizin olduğu şehirlerin nüfusu ve kar oranlarının olduğu bir liste) regresyon metodundan geçirerek nüfusun kar üzerindeki ağırlığını bulabilirsiniz. Daha sonra şube açmak istediğiniz şehrin nüfusuna bağlı olarak o şehirde kar mı, yoksa zarar mı edeceğinizi kestirebilirsiniz.
Şimdi bu eğitim verisini Python da nasıl göstereceğimize bakalım. Bunun için Python da numpy ve matplotlib kütüphanesini kullanacağız. Eğer gerekli kütüphaneleri indirmediyseniz aşağı linklerden indirip kurabilirsiniz. Kurulum ile ilgili kütüphanelerin kendi dökümantasyonu içerisinde anlatımları mevcuttur.
Yukarıdaki kütüphaneleri kurduysanız Python ile veri kümesini aşağıdaki gibi görselleştirebilirsiniz:
1: import numpy as np
2: import matplotlib.pyplot as plt
3: import random
4: def f(x): return 2*x + 4
5: trainX=[]
6: trainY=[]
7: for i in range(0, 50):
8: y = f(i)
9: x = random.choice([i+2, i+1, i, i-0, i-2])
10: trainX.append(x)
11: trainY.append(y)
12: print str(x) + " " + str(y)
13: fig, ax = plt.subplots()
14: ax.plot(trainX, trainY, "r*")
15: plt.show()
Lineer regresyona iki çeşit yaklaşım vardır: Tek Değişkenli Lineer Regresyon ve Çok Değişkenli Lineer Regresyon. Biz burada tek değişkenli lineer regresyondan bahsedeceğiz. Tek değişkenli lineer regresyon aşağıdaki gibi ifade edebiliriz:
Çok değişkenli lineer bir denklemi aşağıdaki gibi ifade edebiliriz:
Burada:
Lineer regresyonda ki amacımız,  değerlerini hesaplamak.
değerlerini hesaplamak.  Değerleri öyle bir seçilmeli ki
Değerleri öyle bir seçilmeli ki 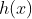 fonksiyonun da hesaplanan tahmin ile gerçek değer olan
fonksiyonun da hesaplanan tahmin ile gerçek değer olan  arasında ki fark(hata) minimum olmalı. Daha teknik bir deyim ile
arasında ki fark(hata) minimum olmalı. Daha teknik bir deyim ile 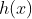 ve
ve  rasındaki farkı gösterecek maliyet fonksiyonunu(cost function) minimum olmalıdır. Maliyet fonksiyonu, şu şekilde ifade edilebilir:
rasındaki farkı gösterecek maliyet fonksiyonunu(cost function) minimum olmalıdır. Maliyet fonksiyonu, şu şekilde ifade edilebilir:
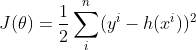 Burada:
Burada:
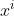 :
:  ’inci satırdaki özellik listesi. Yani,
’inci satırdaki özellik listesi. Yani, 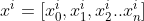
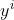 :
:  ’inci satırdaki gerçek değer.
’inci satırdaki gerçek değer.
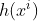 :
:  ’inci satırdaki tahmin edilen değer.
’inci satırdaki tahmin edilen değer.
Yukarıdaki maliyet fonksiyonunu kodlayacak olursak şu şekilde olacaktır:
 değerinin sonuç üzerindeki hatasını bulduk. Ancak amacımız minimum hataya sahip
değerinin sonuç üzerindeki hatasını bulduk. Ancak amacımız minimum hataya sahip  değerlerini belirlemek. Bunun için Gradient Descent metodunu kullanarak fonksiyondaki minimum değeri bulabiliriz. GradientDescent, belirlenen oransal adım büyüklüğü (biz buna öğrenme oranı diyeceğiz.) ile yerel minimum ya da maksimum noktayı hızlı bir şekilde elde etmeye yarayan bir yöntemdir. Genel olarak gradient descent fonksiyonu aşağıdaki gibidir:
değerlerini belirlemek. Bunun için Gradient Descent metodunu kullanarak fonksiyondaki minimum değeri bulabiliriz. GradientDescent, belirlenen oransal adım büyüklüğü (biz buna öğrenme oranı diyeceğiz.) ile yerel minimum ya da maksimum noktayı hızlı bir şekilde elde etmeye yarayan bir yöntemdir. Genel olarak gradient descent fonksiyonu aşağıdaki gibidir:
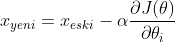 Gradient descent metodunu maliyet fonksiyonuna uyarladığımızda aşağıdaki fonksiyonu elde ederiz:
Gradient descent metodunu maliyet fonksiyonuna uyarladığımızda aşağıdaki fonksiyonu elde ederiz:
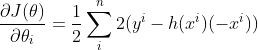
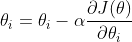
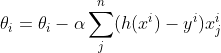 Gradient Descent algoritmasını python ile kodladığımızda aşağıdaki sonucu elde edeceğiz:
Gradient Descent algoritmasını python ile kodladığımızda aşağıdaki sonucu elde edeceğiz:
 Çok küçük belirlendiğinde Gradient Descent algoritması yavaş çalışacaktır.
Çok küçük belirlendiğinde Gradient Descent algoritması yavaş çalışacaktır.
Yukarıdaki maliyet fonksiyonunu kodlayacak olursak şu şekilde olacaktır:
1: def compute_cost(X, y, theta):
2: m = y.size
3: hx = (X.dot(theta).flatten() - y)**2
4: J = ( 1.0 / (2*m)) * hx.sum()
5: return J
1: def gradient_descent(X, y, alpha, theta, iter):
2: m = y.size
3: J_history = np.zeros(shape= (iter, 1))
4: for i in range(iter):
5: hx0 = (X.dot(theta).flatten() - y)
6: hx1 = (X.dot(theta).flatten() - y) * X[:, 1]
7: theta[0,0] = theta[0,0] - alpha * (1.0 / m) * hx0.sum()
8: theta[1,0] = theta[1,0] - alpha * (1.0 / m) * hx1.sum()
9: J_history[i, 0] = compute_cost(X, y, theta)
10: return theta, J_history
 |
Eğer ki  değerini çok büyük belirlersek, algoritma hedeflenen minimum değeri atlayabilir. Bu sebepten minimum noktaya yakınsamak yerine uzaklaşabilir.
değerini çok büyük belirlersek, algoritma hedeflenen minimum değeri atlayabilir. Bu sebepten minimum noktaya yakınsamak yerine uzaklaşabilir.
Eğitim verisinin okunması ve başlangıç parametreleri verilerek Regresyonun çalışması aşağıda verilmiştir:
1: data_set = np.loadtxt('x01.txt')
2: X = data_set[:, 0]
3: y = data_set[:, 1]
4: m = y.size
5: XX = np.ones(shape=(m,2))
6: XX[:, 1] = X
7: alpha = 0.01
8: theta = np.zeros(shape = (2,1))
9: iter = 2000
10: theta, J = gradient_descent(XX, y, alpha, theta, iter)
11: result = XX.dot(theta).flatten()
12: py.scatter(X, y, marker= 'x', c='r')
13: py.plot(X, result)
14: py.show()
Kodu çalıştırdığımızda minimum hataya sahip denklemimiz aşağıda ki gibi olacak:








Hiç yorum yok:
Yorum Gönder